Fabrication Layout
Concept:
The proposal is to supplement/replace shop drawings with a physical layout system based on euclidean coordinates.
Euclidean space is the fundamental space of classical geometry associates with each point an n-tuple of real numbers which locate that point in the Euclidean space and are called the Cartesian coordinates of that point. Euclidean space is the fundamental space of classical geometry. Originally, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any nonnegative integer dimension, [1] including the three-dimensional space and the Euclidean plane (dimension two). It was introduced by the Ancient Greek mathematician Euclid of Alexandria, [2] and the qualifier Euclidean is used to distinguish it from other spaces that were later discovered in physics and modern mathematics.
Ancient Greek geometers introduced Euclidean space for modeling the physical universe.
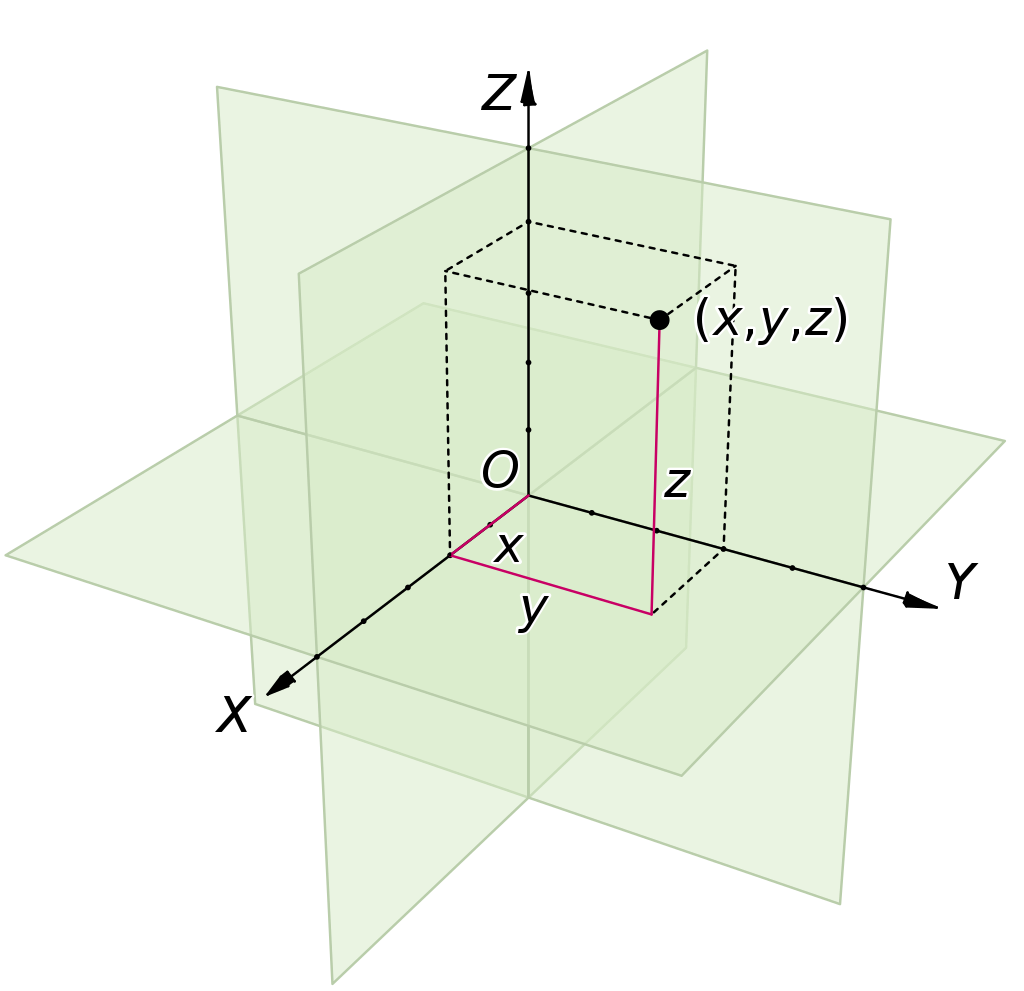
How to locate a point in the Euclidean space using Cartesian coordinates (Graphic above) shows three planes, X,Y,Z. Line lasers are used to create these planes.
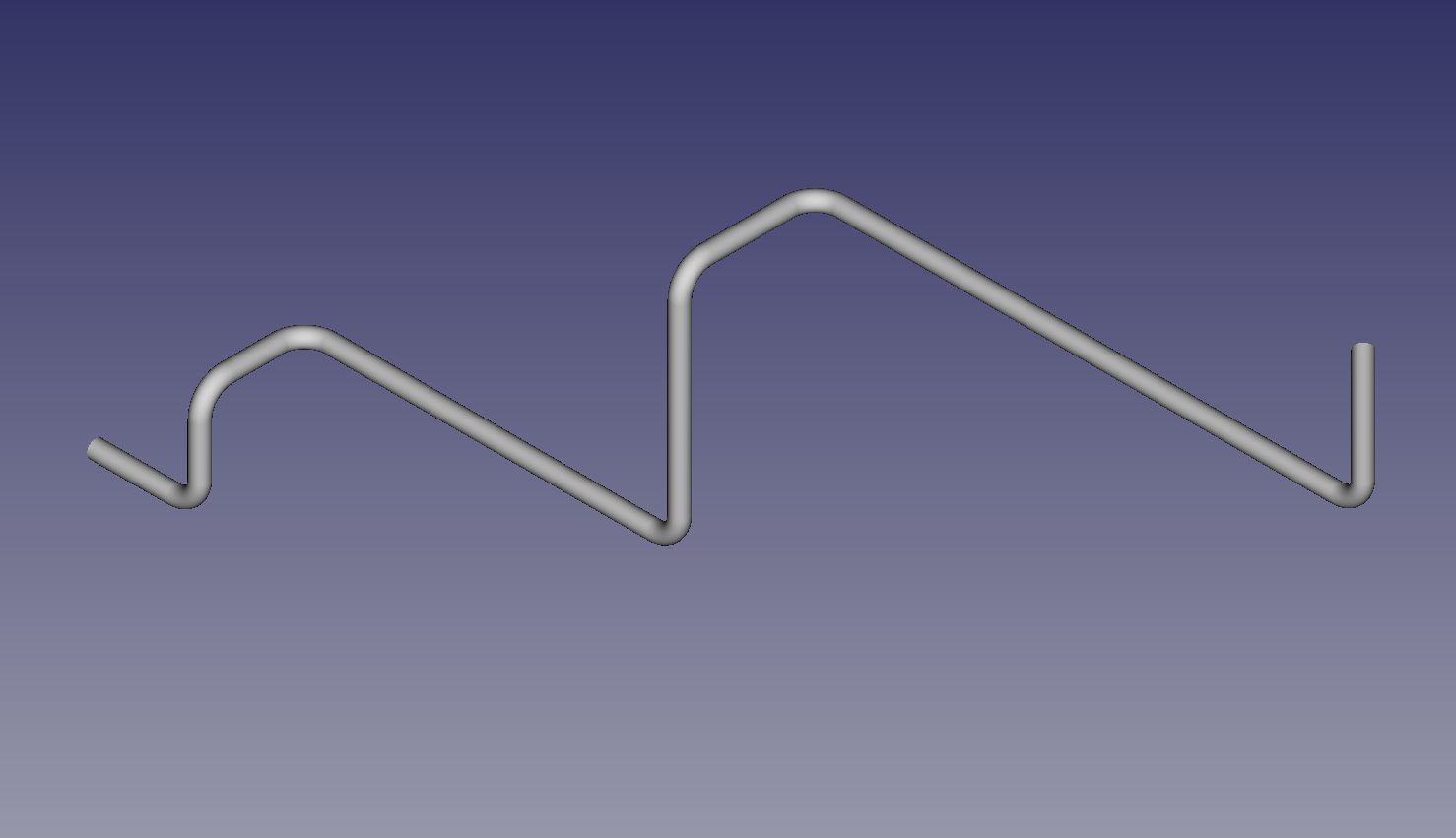
Objective is to fabricate 8 foot to ten foot section of pipe ("spools") using line lasers. Above graphic represents a spool.

Most CAD piping software uses center lines as a basis of pipe geometry. Here the X,Y,Z axis of coordinate 0,0,0 is shown on left.
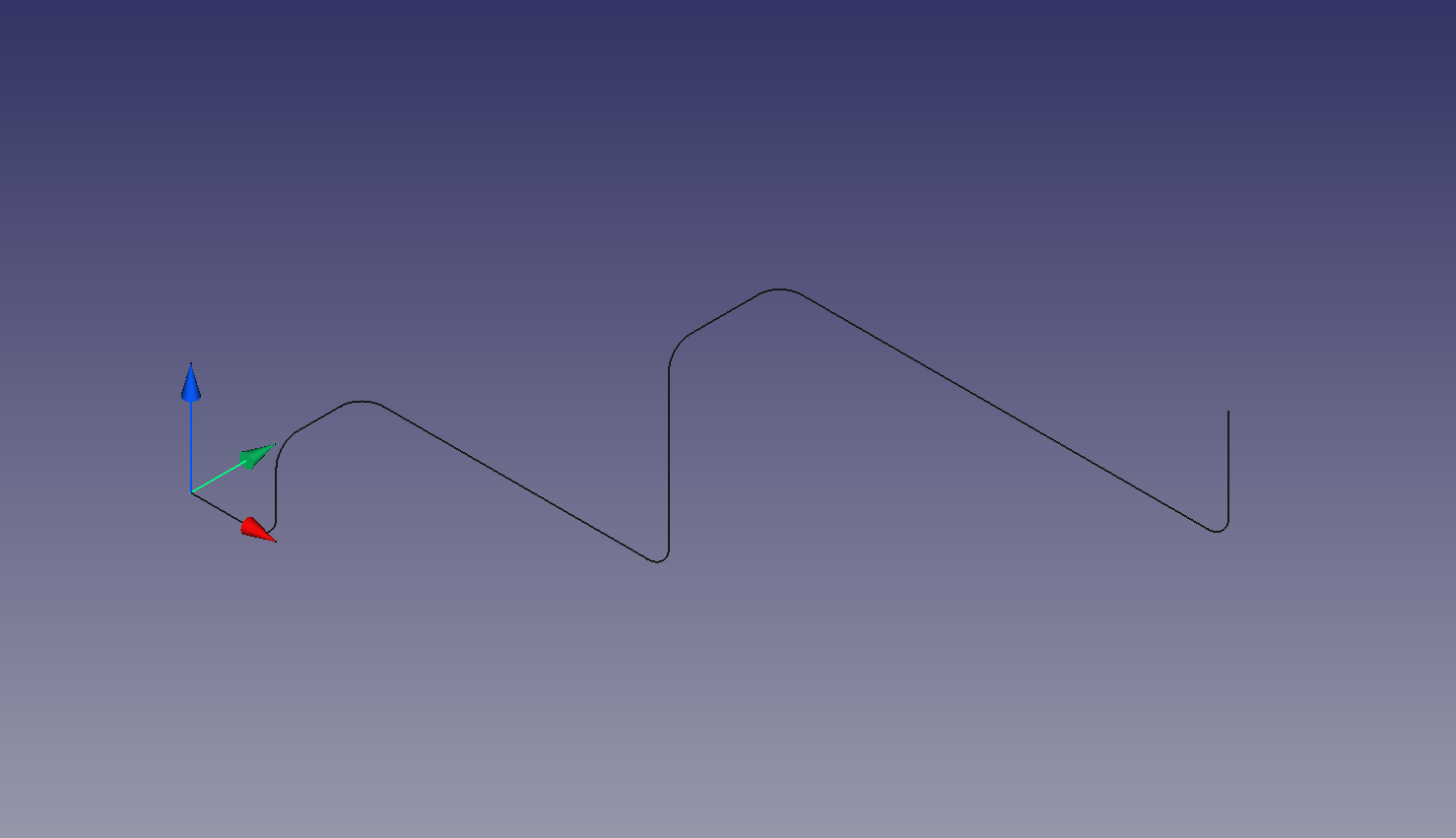
These center lines can be filleted with accurate radius.
Each point has a coordinate defining it's location, here the X,Y coordinate position is shown.
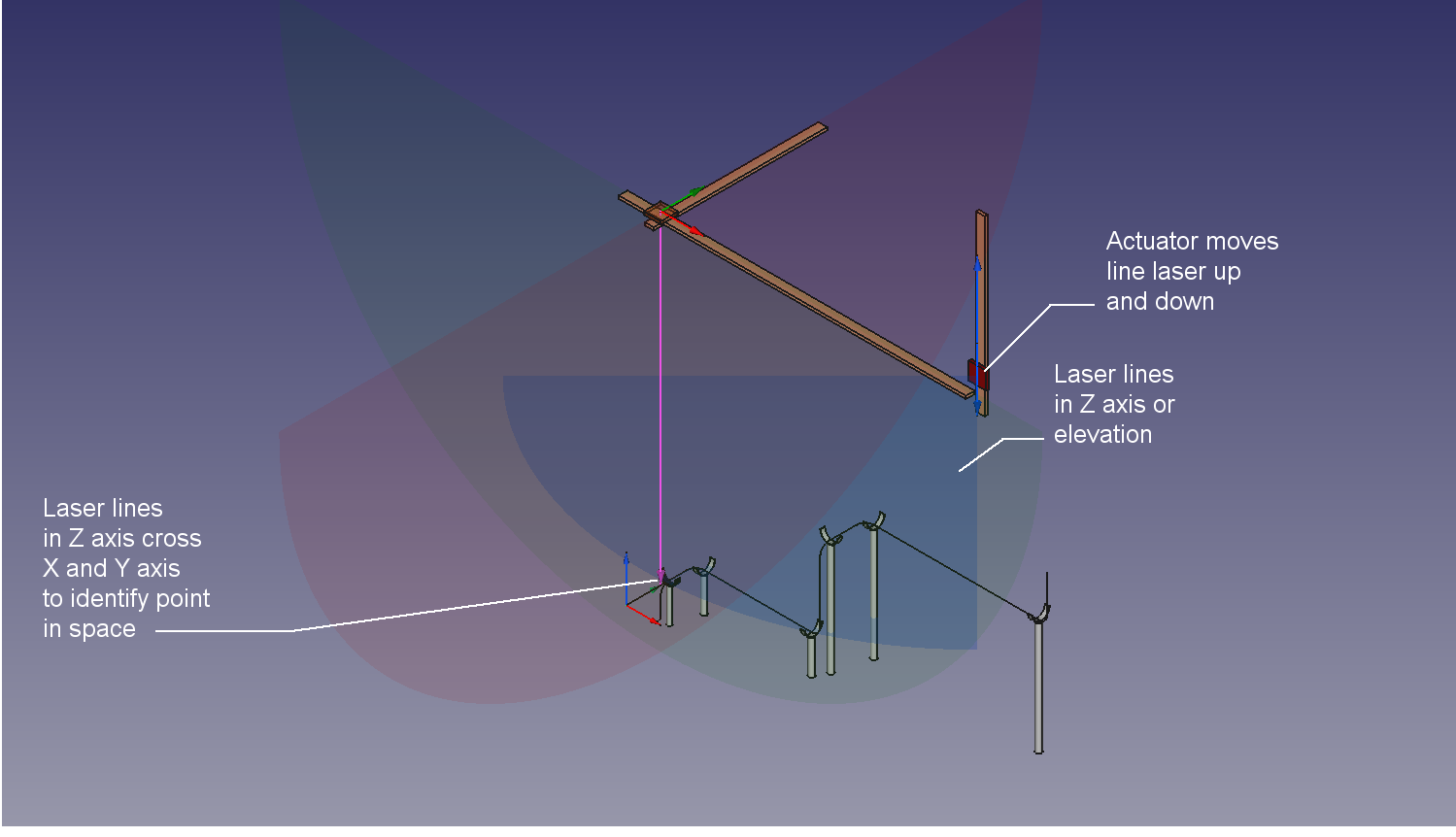
Here the Z coordinate is added.
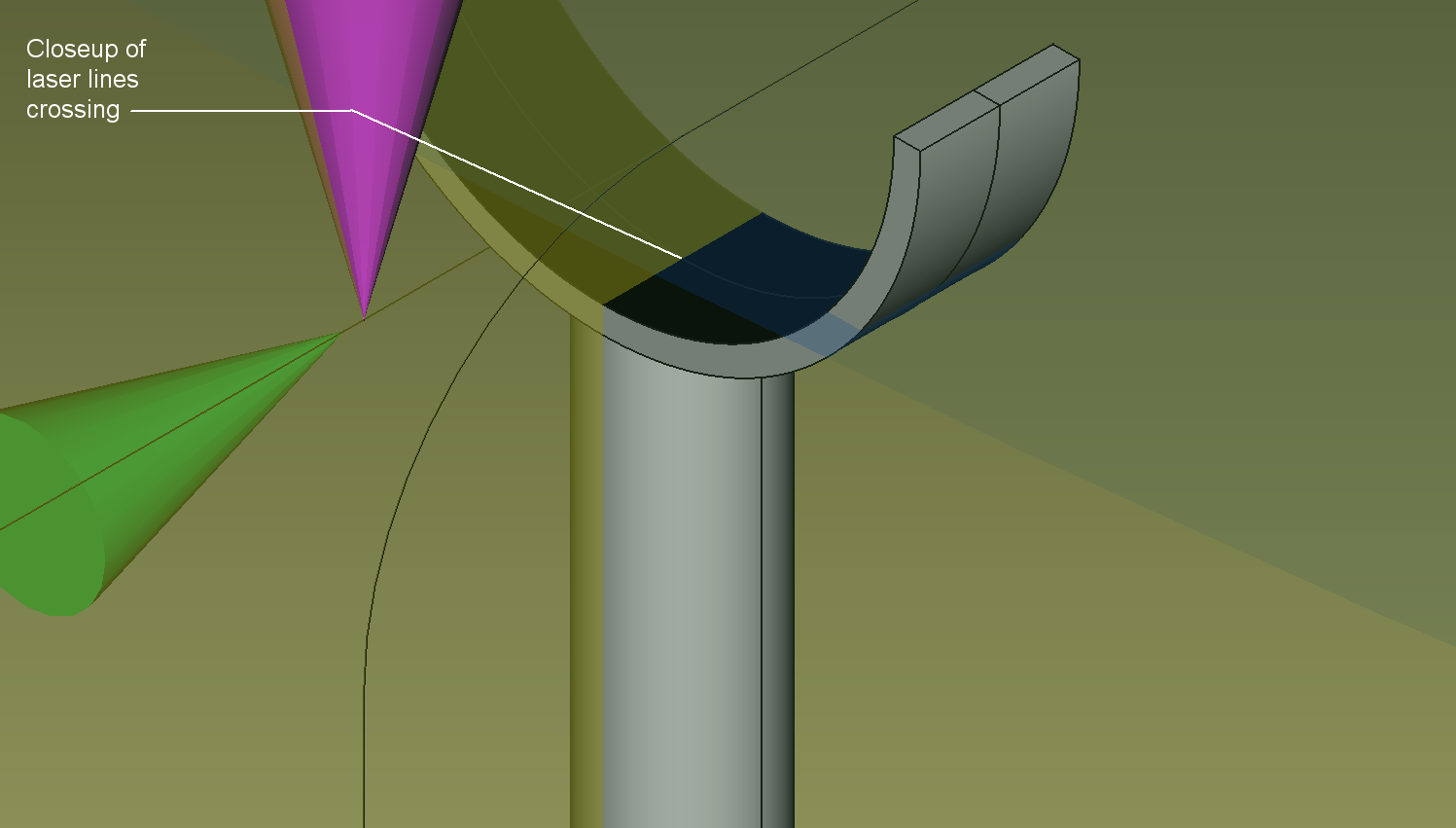
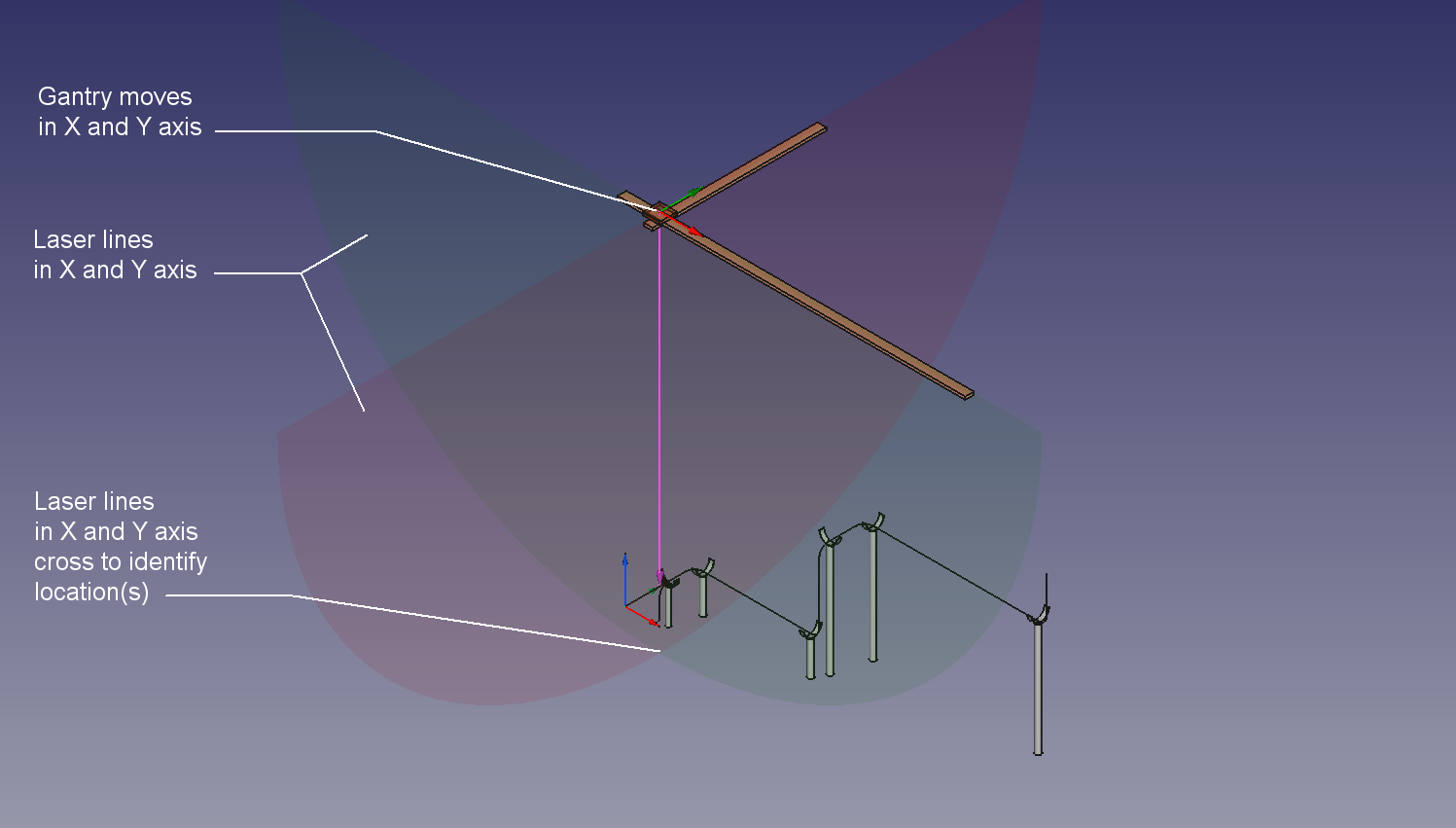
For clarity a close up portrays the laser lines crossing. It should be noted that any item on the pipe can be identified such as valves, ports, hangers.
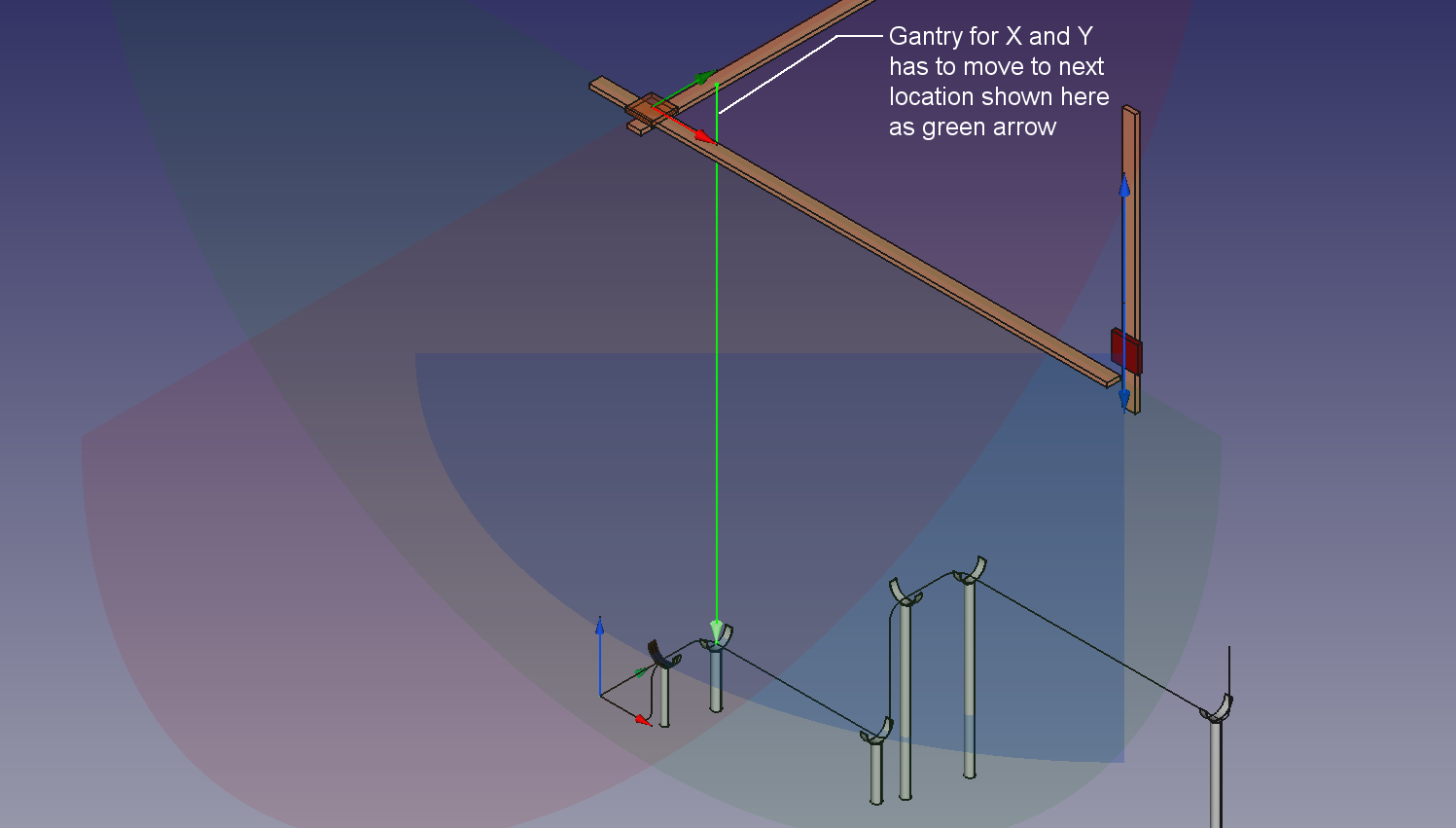
The gantry moves to locate the next section or item to be fabricated.
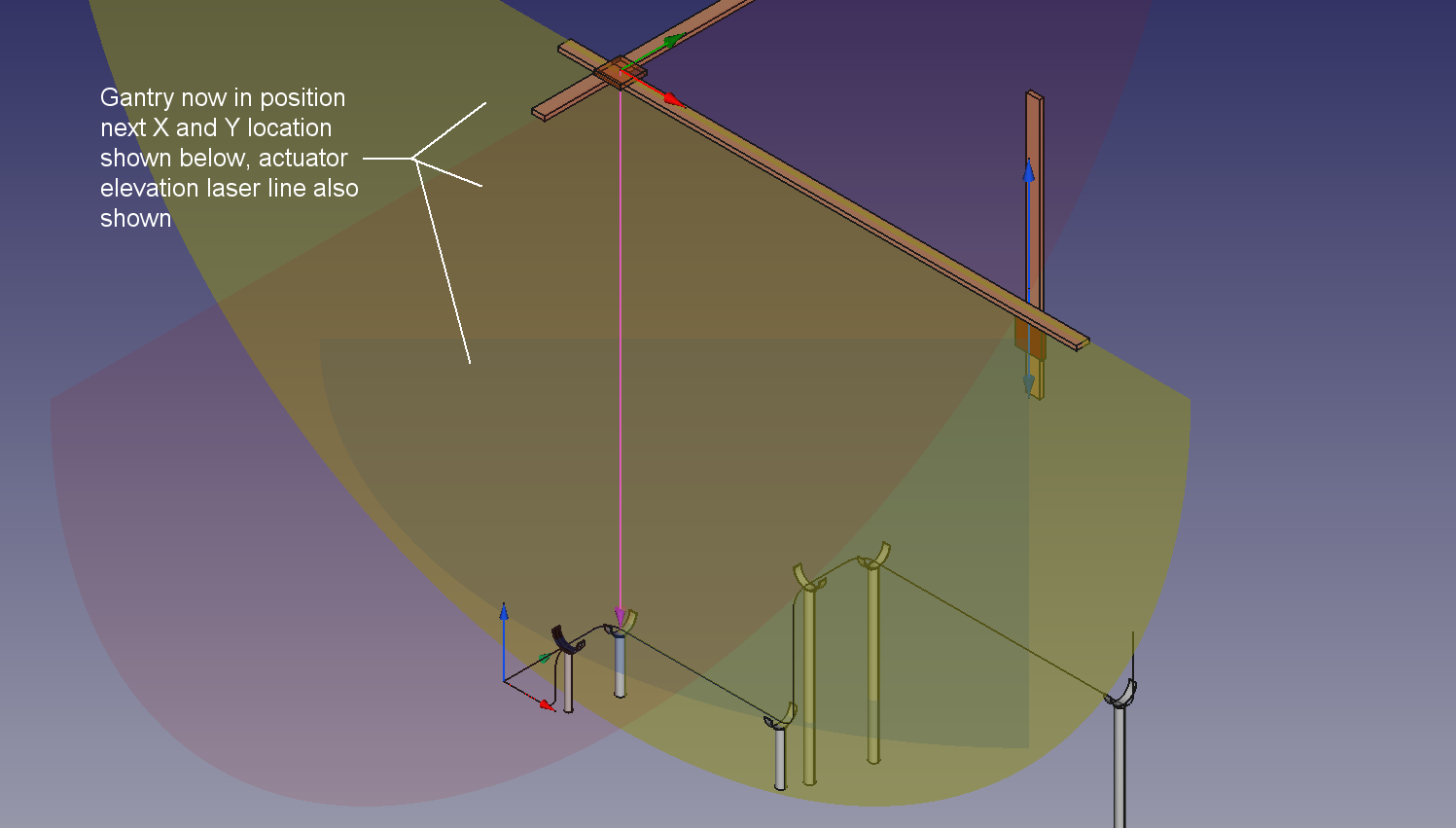
In this example the X,Y,Z coordinates are shown where all laser lines cross.
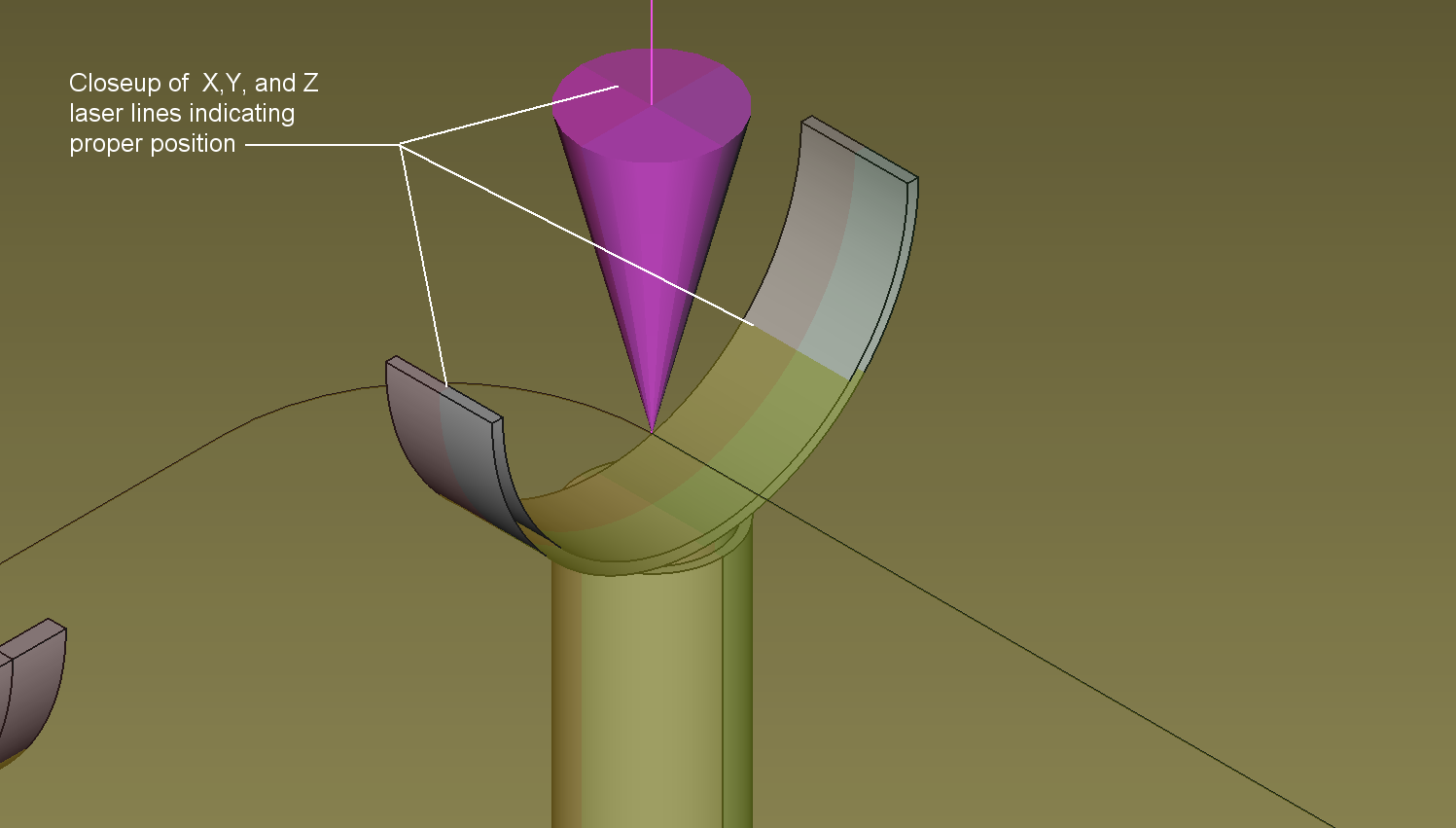
Another closeup of the laser lines crossing at the pipe stand.
References: